超参数搜索

最近遇到了搜索超参数规模过大的问题，需要一些自动调参的方法，下面是一些调研。

前言

这个文档的主要参考资料来自网络，我只是想用这个工具，并没有深入的去研究细节。但是超参数搜索在深度神经网络里面很重要，很多云服务厂商，包括华为云的ModelArts等等，都提供了相应的服务，因此应该还是比较完整的一个调研。

超参数是开始训练之前，用预先确定的值来手动设置的所有训练变量。这里的超参数要区别于训练过程中产生的参数，这些确实也是参数，但是并不需要我们手动设置。下面是一个深度神经网络的例子，图中，学习率、dropout比例以及batch大小就是超参数，但是每层神经网络的参数，虽然也很重要，但是我们并不很关心，也不需要我们手动去设置，因此就不是超参数。

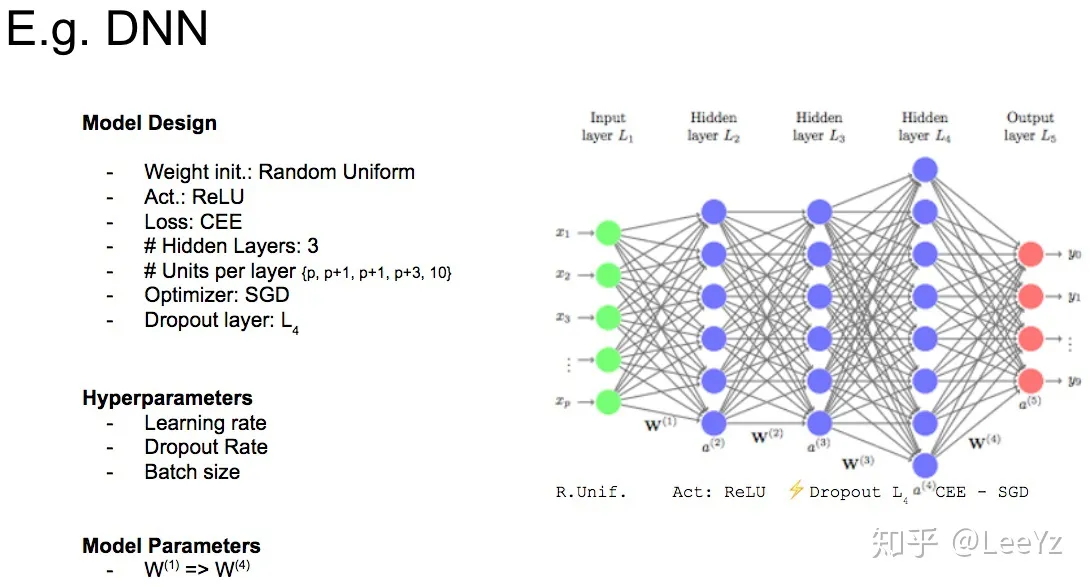
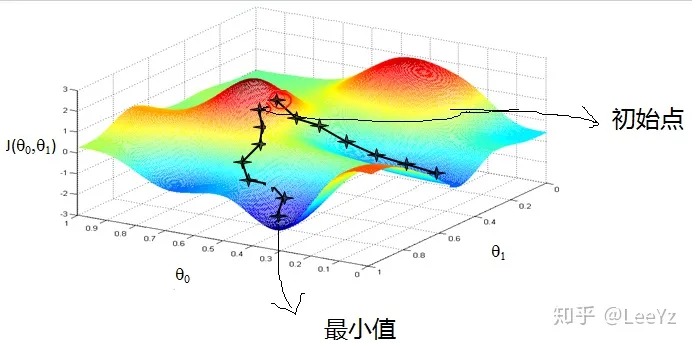
训练过神经网络的都知道，调参是一门玄学，是需要不断设计优化并且有一定的理论支持的。之所以会这样，我认为主要是因为我们梯度下降法，虽然最后或许能收敛到某个极小点，但是是否能到达，会不会走过了，能不能到某一个固定的极小值点，其实都是不确定的。这些都依赖于参数的选择，目前还没有很好的解决方法。例如下图就给了两个不同的路径，不断优化之后函数确实收敛了，但是得到的结果是截然不同的。

而超参数搜索就是一个找到最优超参数的过程，这是很多机器学习从业者的追求，但是也面临着很多困难。目前有一些搜索方法，大致可以总结为以下几个：

• Babysitting
• Grid Search
• Random Search
• Optimization

Babysitting

Babysitting是最常用的方法，纯手工操作。简单点讲，这个方法就是玄学调参。

具体来讲，babysitting的方法就是手动的设置一个参数，然后根据一些经验来判断这些参数的好坏，然后在时间还足够的情况下不断地去优化改进。上面是一个经典的机器学习的流程图，如果我们也是基于机器学习的方法去调参的话，我们每次就都需要将这一流程重新都一遍，并根据经验去判断。

一般来说这一方法还是挺好用的，因为在不同的任务上总有一定的经验知识。特别是学生在初学的时候，这个过程也很有利于学生对算法的理解(和摸鱼)，但是显然这不是很好的方法，也很不自动化。

Grid Search

好，现在我们要开始自动搜索了。之前babysitting方法，我们其实是心里面有一个可行的参数范围，然后根据一些经验不断地去尝试更好的方法。那么一个最直接的自动搜索方法就是，我直接把我心里面的可行的参数范围都搜一遍就可以了。这就是Grid Search。这其实就是一个遍历的思路，之所以叫Grid Search，可以看下图。

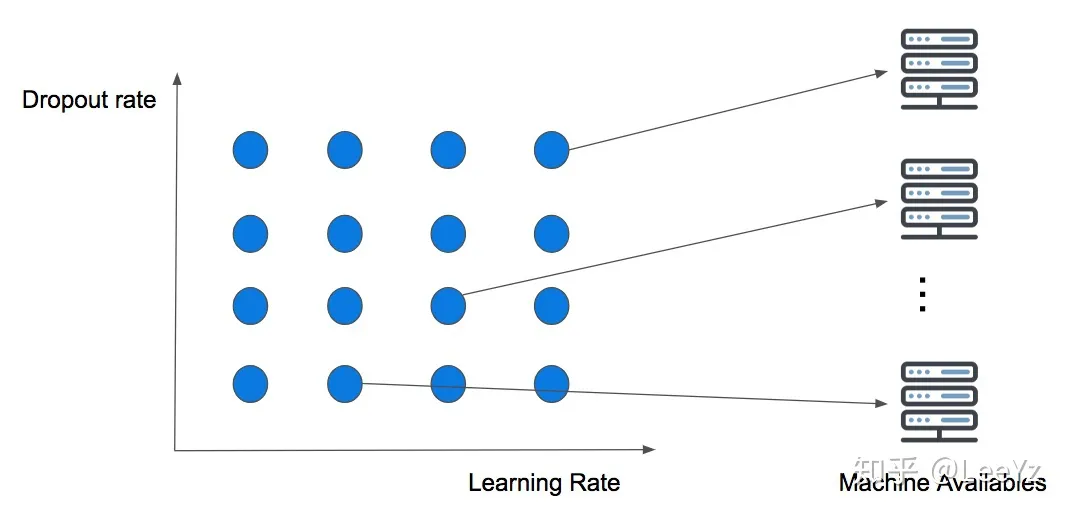
例如我们现在要对学习率和dropout的比例进行遍历，那应该是两层循环。这意味着我们需要将两个参数可能出现的值的各种组合都试一遍，那不就构成了一个Grid吗。

这个方法有多个好处。首先，我们将所有可能的情况都试了一遍，那么其实我们可以说，我们找到了最优解了；其次，在不考虑计算资源限制的情况下，这些参数调试的计算其实是可以并行进行的，这意味着我们可以用空间换时间。如果做一次实验需要的时间是1ms，那么这并不重要；但是现在的大规模神经网络训练动辄好几天甚至一周，那么这就很重要了。

Random Search

计算机科学里面有一些很有趣的现象，有的时候我们精心设计的方案还没有我们随机搜一个效果好，例如这个随机搜索。

我们考虑下面左图的网格搜索，看上去每种情况都已经考虑到了，但是其实并不然。网格搜索其实也只是搜索了这么一个子空间的一小部分，准确的说是那几个点。我们认为当网格足够密集的时候，可以认为遍历了整个子空间，但是网络越密集，搜索代价越大，在同样的搜索成本下，我们只能搜有限的几个点，这个时候效率就显得比较重要了。

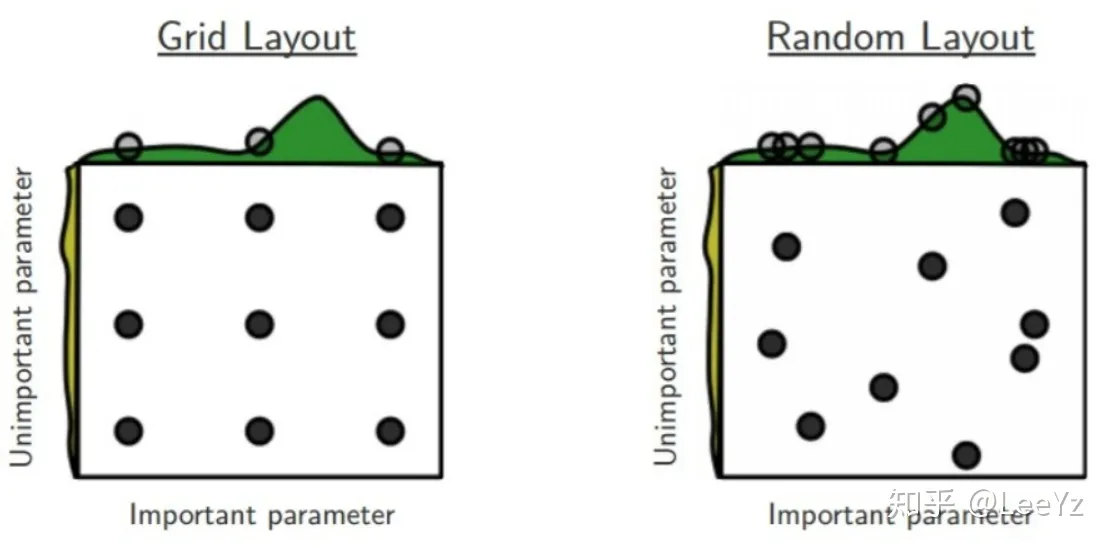
图中，同样是搜9个点，网格搜索的情况下，重要的参数其实只取了三个不同的值，这其实效率并不高，因为有的时候网络的效果只和这个参数有关，所以只相当于做了三次实验。而如果随机搜索的话，那么可以看出，我随机得到的点，重要的参数取到了9个不同的值，显然效果更高。

Optimization

但是这些搜索方法其实还是存在组合爆炸的问题，规模一大，就很难cover住所有的结果了，这个时候，优化的方法就显得比较重要了。目前公认的效果比较好的优化方法是贝叶斯优化，此外，基于进化算法的优化也较为常见。

优化的方法的思路是这样的。假设我们现在有一个函数$f:x\to R$，我们需要在$x \subseteq X$内找到 $$ x^* = \arg\min_{x \in X}f(x) $$ 其中，$x$为超参数，$X$为问题的定义域。显然，当凸的时候，我们可以使用凸优化的方法来解决这一问题，但是，现在我们面临的问题往往是expensive black-box function，这就遇到了困难。

贝叶斯优化

Sequential model-based optimization (SMBO) 是贝叶斯优化的最简形式，其算法思路如下：

简单来讲，就是采用一个模型在现有的数据点上不断地去逼近，每次选到的最好结果都加入现有的数据点中再进行拟合。贝叶斯优化往往采用高斯模型去拟合，当然也有一些变种，在此不进行展开。

大致示意图如下所示，本来是用一个高斯模型去拟合，每加一个点，不确定性就增大一些。

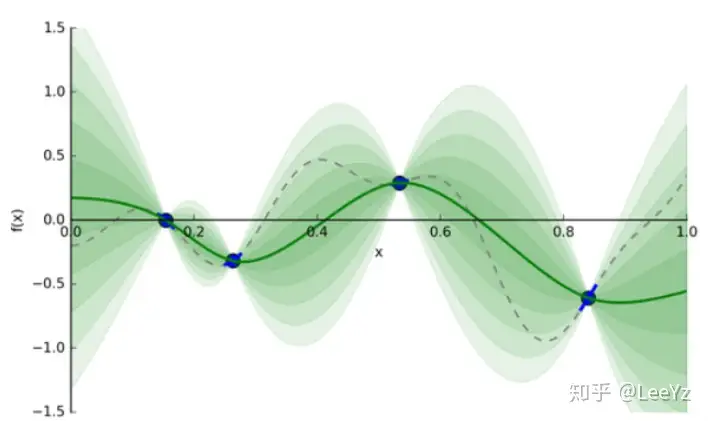
假设我可以做无穷多次实验，那么我这个拟合就可以很准确。如果我只能做几次实验，那么我的结果也不会很准确。这里就存在一个取舍问题了。

进化算法优化

进化算法是一类仿生算法，借鉴了生物进化过程中的一些特性，是一种比较鲁棒的优化算法，包含很多类别，例如遗传算法、粒子群算法等等，大致思路都差不多。

例如遗传算法，就是模拟了遗传这一过程。下图展示了这一模拟。首先我们会初始化一些基因，然后会选择表现比较好的基因作为父方和母方，进行遗传操作。基因的遗传操作包括交叉与变异，交叉保证了基因的遗传，变异保证了新的基因的出现，因此都是有必要的。然后我们再对产生的新的基因进行评估，重复这一过程，直到收敛。

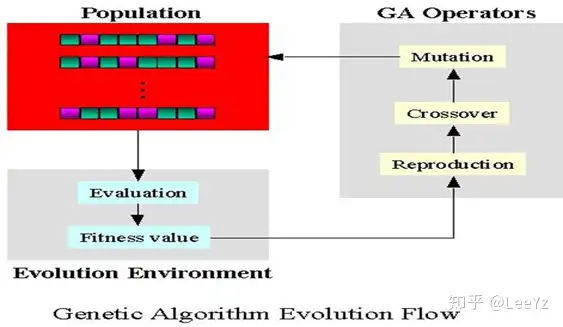
经历这一过程，我们便可以较为快速地对参数进行优化。但是显然，这一优化的结果并不保证是最优的。

后记

这篇文章对现有的超参数优化的方法进行了一些简单的调研。由于NAS专注于神经网络架构的搜索，本文旨在解决超参数搜索的问题，不局限于神经网络，因此并没有提到。现有的超参数优化方法其实都还比较初级，还没有一个很好的方法去搜索超参数，各个方法都有自己的优势与劣势。即使是最简单的babysitting方法，也有可以带入专家经验的优势在里面。因此在实际使用过程中，我们还是需要按照自己的需要灵活。

参考文献

[1]《深度学习超参数搜索实用指南》, 知乎专栏. https://zhuanlan.zhihu.com/p/46278815 (见于 11月 21, 2020).

[2]《贝叶斯优化(Bayesian Optimization)深入理解》, 知乎专栏. https://zhuanlan.zhihu.com/p/53826787 (见于 11月 21, 2020).

[3]《梯度下降（Gradient Descent）小结 - 刘建平Pinard - 博客园》. https://www.cnblogs.com/pinard/p/5970503.html (见于 11月 21, 2020).

[4]《遗传算法和超参数优化》, 知乎专栏. https://zhuanlan.zhihu.com/p/123319468 (见于 11月 21, 2020).

[5]《遗传算法详解（GA）boat_lee的博客-CSDN博客_遗传算法》. https://blog.csdn.net/u010451580/article/details/51178225 (见于 11月 21, 2020).